[백준알고리즘] 11051번: 이항계수 2 -C
https://www.acmicpc.net/problem/11051
11051번: 이항 계수 2
첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 1,000, 0 ≤ \(K\) ≤ \(N\))
www.acmicpc.net
하지만 범위가 훨씬 더 커졌기 때문에 아까와 같은 방식으로 하려고 하면 int의 범위를 넘어서 overflow를 일으킬 것이다. double의 경우는 해보지 않았지만 속도가 느릴 것이다.
하지만 여기서는 모듈러 연산(Modular Arithmetic: 나머지 연산)을 이용해서 int범위 안에서 돌아가도록 할 것이다.
문제를 주었을 때 10007로 나눈 나머지를 구하라고 했기 때문에 가능한 연산이다.
모듈러 자체의 특징에 대해서는 링크를 따로 보도록 하는 것이 좋을 것 같다. 모듈러 연산에는 다음과 같은 대표적인 특징이 있다.
1. (a + b) mod n = ((a mod n) + (b mod n)) mod n
2. (a - b) mod n = ((a mod n) - (b mod n)) mod n
3. (a * b) mod n = ((a mod n) * (b mod n)) mod n
모듈러 안의 연산은 위와 같이 분배 법칙과는 조금 다른 저러한 형태를 만족한다는 것이다.
그렇기 때문에 각 연산의 결과를 모두 모듈러 해서 저장을 하면 int의 범위 안(여기서는 10007의 범위 안)에서 다룰 수 있는 것이다.
여기서 이항 계수의 식을 한번 봐보도록 하자.
nCk = n! / (k! * (n-k)!)
이 식에서 10007로 나눈 나머지를 보이라고 했으니까 다음과 같은 식일 것이다.
nCk % 10007 = n! / (k! * (n-k)!) % 10007
그럼 우변을 위에서 봤던 모듈러 연산의 속성을 이용해보도록 하ㅈ....?
위의 모듈러 연산의 속성에서는 나눗셈에 대한 연산이 적혀있지 않다.
그럼 나눗셈을 곱셈으로 바꿔서 보도록 하자!
n! / (k! * (n-k)!) % 10007
= ((n! % 10007) * ((k! * (n-k)!)^-1 % 10007)) % 10007
k! * (n-k)! 에 대해서 역원을 취했다.
그럼 이제 이 역원을 어떻게 구할 것인지가 또 문제가 될 것이다.
일반적인 곱셈에서 정수 x의 역원은 x * y = 1을 만족하는, 곱해서 1이 되는 y일 것이다.
모듈러 곱셈 연산에서의 역원은 (x * y) % n = 1 % n을 만족하는, 곱해서 n으로 모듈러를 취했을 때 나머지가 1인 y이다. 이 수를 구하기 위해서 모든 수를 1부터 넣어가면서 구해도 되겠지만, 빠르게 구하는 공식이 있다.
페르마의 소정리와 오일러 정리이다. (암호학 수업 때 들었던걸 포스팅하면서 새로 정리하려 했는데, 수학식 쓰는 문제도 있고.... 정리가 굉장히 잘되어있어서 링크를 걸었다.)
코드를 작성할 때에는 10007이 소수이기 때문에 간단히 페르마의 소정리를 이용했다. 오일러 정리를 이용해서 풀려면 오일러 함수에 대한 부분도 작성해야 했기 때문에...
참고로 오일러 정리를 이용하면 밑에서 나오는 방법 말고 빠른 지수 연산도 가능하다.
그럼 여기까지 왔다면 (n! % 10007)은 문제가 없을 것이고, ((k! * (n-k)!)^-1 % 10007)) = ((k! * (n-k)!)^10005 % 10007))라는 것 까지 왔을 것이다.
그런데 저 10005 제곱을 언제 다하고 있을 것인가... 여기서는 방금 위에서도 말했듯이 빠른 지수 연산을 이용할 것이다. 여기서는 별다른 특별한 트릭은 존재하지 않는다. 그저 (x * x = x^2)이고 (x^2 * x^2 = x^4)인 간단한 원리를 이용해서 한 것이다. 당연히 저 과정에도 모듈러 연산은 들어가야 한다. ( ( (x^2) % n) * ( (x^2) % n) ) % n = (x^4) % n)이 되어야 한다. 이유는 링크 안의 사이트에서 잘 설명이 되어있다.
그럼 이제 우리가 여태 정리했던 내용을 코드로 구현해보도록 하자.
이항 계수를 구하기 위한 식을 사용하면서 10007로 나눈 나머지를 구하기 위해서 다음의 식을 사용했다.
nCk % 10007 = n! / (k! * (n-k)!) % 10007
여기서 나눗셈을 곱셈으로 바꿔주고 모듈러 연산을 사용하기 위해서 (k! * (n-k)!)의 역원을 구해줬다.
역원은 (k! * (n-k)!)^10005이며, 이 식을 구하기 위해서 빠른 지수 연산을 이용하면서 모듈러 연산을 이용해줬다.
모듈러 연산을 포함한 식은 ((k! * (n-k)!)^10005) % 10007을 구하는 것이다. 그렇기 때문에 여기서도 모듈러 연산의 곱셈 속성을 이용해서 범위 안에서 구할 수 있다.
다 구하게 된다면 ((n! % 10007) * ((k! * (n-k)!)^-1 % 10007)) % 10007에 필요한 값들을 채워 넣을 수 있게 된다.
#include <stdio.h>
int N, K;
int factorial_arr[1001];
void factorial(void);
int divisor(void);
int main(void){
int d;
scanf("%d", &N);
scanf("%d", &K);
if(K < 0 || K > N){
printf("0\n");
return 0;
}
factorial();
d = divisor();
printf("%d\n", (factorial_arr[N] * d) % 10007);
return 0;
}
void factorial(void){
int i;
factorial_arr[0] = 1;
for(i = 1; i <= 1000; i++){
factorial_arr[i] = (factorial_arr[i - 1] * i) % 10007;
}
return;
}
int divisor(void){
/* find (K!*(N-K)!)^10005 % 10007 */
/* 8192 = 2^13 */
int divisor_arr[14];
int exponential[14];
int i, ret = 1, target = 10005;
exponential[0] = 1;
for(i = 1; i < 14; i++){
exponential[i] = exponential[i - 1] * 2;
}
// 각 지수에 해당하는 모듈러 값
divisor_arr[0] = (factorial_arr[K] * factorial_arr[N - K]) % 10007;
for(i = 1; i < 14; i++){
divisor_arr[i] = (divisor_arr[i - 1] * divisor_arr[i - 1]) % 10007;
}
i = 13;
while(target != 0){
if(target >= exponential[i]){ // target값을 맞추기 위해서 뺄 수 있을 때마다 빼버림
target -= exponential[i];
ret *= divisor_arr[i];
ret %= 10007;
}
i--;
}
return ret;
}
divisor함수에 대해서만 간단히 설명을 하자면 10005 제곱을 구하기 위해서 1, 2, 4, 8, 16,... 8192까지만 구하고 이들이 지수로 올라가서 10005를 더해서 만들 수 있는 값들을 모듈러 곱연산을 한 것이다. 8192까지 구한 이유는 한번 더 진행하면 16384까지 가는데 어차피 10005를 넘기 때문에 구성에 포함할 수 없기 때문이다. 더해서 10005를 만들수 있는 값들을 곱연산 시킨 이유는 x^1 + x^2 = x^(1 + 2) = x^3의 속성때문에 10005제곱을 구하기 위해서 8192 +... 를 구한 것이고 ret에서는 곱한 것이다. (exponential[]로 지수만 비교한 후 진짜 값은 곱해줘야 하기 때문)
그리고 다른 분들은 다들 dp를 사용하신 것 같으니 다른 분들의 코드도 확인해보는 것이 좋을 것 같다.
dp를 사용한 방법은 좀 더 간단하지만 제출한 풀이들의 시간을 보면, 내 방식이 시간복잡도가 O(n)이지만 dp로 한 방법들은 O(n^2)정도로 만들어진 것 같아서 좀 더 빠른 것 같다.
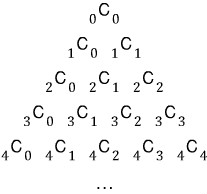
dp를 사용한 방법은 파스칼의 삼각형을 이용해서 푼 것들이다.
<참고>
https://noasax.github.io/problem%20solving/2017/09/24/Division-in-modular.html
잘못된 점이나 부족한 점 지적해주시면 감사하겠습니다
'algorithm > 백준알고리즘' 카테고리의 다른 글
| [백준알고리즘] 1676번: 팩토리얼 0의 개수 -Python (1) | 2019.09.04 |
|---|---|
| [백준알고리즘] 9375번: 패션왕 신해빈 -Python (1) | 2019.09.04 |
| [백준알고리즘] 11050번: 이항계수 1 -C (0) | 2019.09.03 |
| [백준알고리즘] 3036번: 링 -C (0) | 2019.09.03 |
| [백준알고리즘] 2981번: 검문 -Python (0) | 2019.09.02 |