[백준알고리즘] 2104번: 부분배열 고르기-C++
10090번: Counting Inversions (acmicpc.net)
10090번: Counting Inversions
A permutation of integers from 1 to n is a sequence a1, a2, ..., an, such that each integer from 1 to n is appeared in the sequence exactly once. Two integers in а permutation form an inversion, when the bigger one is before the smaller one. As an example
www.acmicpc.net
문제를 오랜만에 풀었다. 전에 풀려고 미리 좀 봤었는데 이리저리 바쁜 일정들로 인해 잊고 살았었다.
다시 보니까 푸는 방법이 기억나지 않아서 다른 사람들의 풀이를 보고 다시 복기했다.
문제는 영어로 쓰여있지만 그렇게 어려운 말들이 아니라서 해석하는데 어려움은 없다.
복기하면서 보니까 예전에 이런 유형의 문제를 풀었던 것 같았다. 무슨 문제인지는 정확히 기억나지는 않는다.
문제 풀이
주어진 순열을 정렬할 때 문제를 쉽게 풀 수 있다. 다음과 같이 주어진 순열을 정렬된 형태로 만들 때 생기는 교차점이 Inversion의 총 개수다.
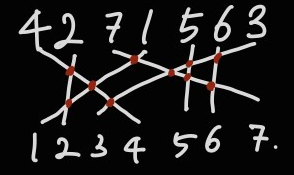
빠른 정렬 알고리즘이면서 이 교차점을 찾기 쉬운 정렬 알고리즘은 Merge Sort다. 그래서 아래 그림과 같이 합병 정렬을 통해 Inversion 횟수를 구할 것이다.

각 conquer 단계에서 오른쪽 분할에 위치한 값이 정렬 대상으로 선택될 때 남아있는 왼쪽 분할의 값의 개수만큼 Inversion이 있다.
이렇게만 하면, Merge Sort만 할 수 있다면 문제를 풀 수 있다. 합병 정렬을 생각하기 까지가 되게 오래 걸리긴 하지만..
#include <cstdio>
int permutation[1000001];
int sorted[1000001];
size_t inputPermutationSize();
void inputPermutation(const size_t siPermutation);
unsigned long long countInversion(const size_t siPermutation);
void printInversion(const unsigned long long ullCount);
int main(void) {
const size_t siPermutation = inputPermutationSize();
inputPermutation(siPermutation);
const unsigned long long ullCount = countInversion(siPermutation);
printInversion(ullCount);
return 0;
}
size_t inputPermutationSize() {
size_t size;
::scanf("%zu", &size);
return size;
}
void inputPermutation(const size_t siPermutation) {
for ( size_t siCount = 0; siCount < siPermutation; ++siCount ) {
::scanf("%d", &permutation[siCount]);
}
}
unsigned long long divideAndConquer(const size_t siStart, const size_t siEnd) {
if ( siStart >= siEnd ) {
return 0;
}
const size_t siMid = (siStart + siEnd) / 2;
unsigned long long ullInversion = 0;
ullInversion += divideAndConquer(siStart, siMid);
ullInversion += divideAndConquer(siMid + 1, siEnd);
size_t siLeft = siStart;
size_t siRight = siMid + 1;
size_t siSorted = siStart;
while ( siLeft <= siMid && siRight <= siEnd ) {
if ( permutation[siLeft] < permutation[siRight] ) {
sorted[siSorted++] = permutation[siLeft++];
}
else {
ullInversion += (siMid - siLeft + 1);
sorted[siSorted++] = permutation[siRight++];
}
}
while ( siLeft <= siMid ) {
sorted[siSorted++] = permutation[siLeft++];
}
while ( siRight <= siEnd ) {
sorted[siSorted++] = permutation[siRight++];
}
for ( siSorted = siStart; siSorted <= siEnd; ++siSorted ) {
permutation[siSorted] = sorted[siSorted];
}
return ullInversion;
}
unsigned long long countInversion(const size_t siPermutation) {
return divideAndConquer(0, siPermutation - 1);
}
void printInversion(const unsigned long long ullCount) {
::printf("%llu", ullCount);
}